GPU推理提速4倍，256K上下文全球最长：无问芯穹刷新大模型优化记录

想用大模型赚钱？这个实力强劲的新面孔决定先把推理成本打下来。

原文来源：机器之心

图片来源：由无界 AI生成

大模型业务到底多烧钱？前段时间，华尔街日报的一则报道给出了参考答案。

报道显示，微软的 GitHub Copilot 业务（背后由 OpenAI 的 GPT 大模型支撑）虽然每月收费 10 美元，但平均还是要为每个用户倒贴 20 美元。可见当前 AI 服务提供商们正面临着严峻的经济账挑战 —— 这些服务不仅构建成本高昂，运营成本也非常高。

有人比喻说：「使用 AI 总结电子邮件，就像是让兰博基尼送披萨外卖。」

对此，OpenAI 算过一笔更详细的账：当上下文长度为 8K 时，每 1K 输入 token 的成本为 3 美分，输出的成本为 6 美分。目前，OpenAI 拥有 1.8 亿用户，每天收到的查询数量超过 1000 万次。这样算来，为了运营 ChatGPT 这样的模型，OpenAI 每天都需要在必要的计算硬件上投入大约 700 万美元，可以说是贵得吓人。

降低 LLM 的推理成本势在必行，而提升推理速度成为一条行之有效的关键路径。

实际上，研究社区已经提出了不少用于加速 LLM 推理任务的技术，包括 DeepSpeed、FlexGen、vLLM、OpenPPL、FlashDecoding 和 TensorRT-LLM 等。这些技术自然也各有优势和短板。其中，FlashDecoding 是 FlashAttention 作者、斯坦福大学团队的 Tri Dao 等人在上个月提出的一种 state-of-the-art 方法，它通过并行加载数据，大幅提升了 LLM 的推理速度，被认为极具潜力。但与此同时，它也引入了一些不必要的计算开销，因此依然存在很大的优化空间。

为了进一步解决问题，近日，来自无问芯穹（Infinigence-AI）、清华大学和上海交通大学的联合团队提出了一种新方法 FlashDecoding++，不仅能带来比之前方法更强的加速能力（可以将 GPU 推理提速 2-4 倍），更重要的是还同时支持 NVIDIA 和 AMD 的 GPU！它的核心思想是通过异步方法实现注意力计算的真正并行，并针对「矮胖」矩阵乘优化加速 Decode 阶段的计算。

论文地址：https://arxiv.org/pdf/2311.01282.pdf

将 GPU 推理提速 2-4 倍，

FlashDecoding++ 是怎么做到的？

LLM 推理任务一般为输入一段文字（token），通过 LLM 模型计算继续生成文字或其他形式的内容。

LLM 的推理计算可被分为 Prefill 和 Decode 两个阶段，其中 Prefill 阶段通过理解输入文字，生成第一个 token；Decode 阶段则顺序输出后续 token。在两个阶段，LLM 推理的计算可被分为注意力计算和矩阵乘计算两个主要部分。

对于注意力计算，现有工作如 FlashDecoding 切分注意力计算中的 softmax 算子实现并行加载数据。这一方法由于需要在不同部分 softmax 同步最大值，在注意力计算中引入了 20% 的计算开销。而对于矩阵乘计算，在 Decode 阶段，左乘矩阵多表现为「矮胖」矩阵，即其行数一般不大（如 <=8），现有 LLM 推理引擎通过补 0 将行数扩充到 64 从而利用 Tensor Core 等架构加速，从而导致大量的无效计算（乘 0）。

为解决上述问题，「FlashDecoding++」的核心思想在于，通过异步方法实现注意力计算的真正并行，并针对「矮胖」矩阵乘优化加速 Decode 阶段的计算。

异步并行部分 softmax 计算

图 1 异步并行部分 softmax 计算

先前工作对每个部分 softmax 计算求输入最大值作为缩放系数，避免 softmax 计算中 e 指数的溢出，这就导致了不同部分 softmax 计算的同步开销（图 1 (a)(b)）。

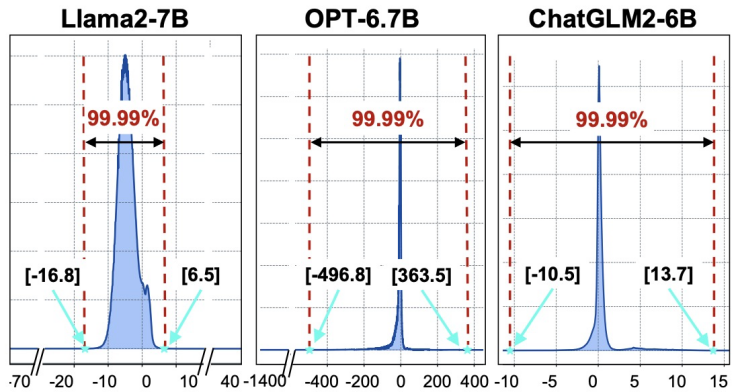
图 2 softmax 输入值统计分布

「FlashDecoding++」指出，对于大部分 LLM，其 softmax 的输入分布较为集中。如图 2 所示，Llama2-7B 的 softmax 输入 99.99% 以上集中在 [-16.8, 6.5] 这个区间。因此，「FlashDecoding++」提出在部分 softmax 计算时使用一个固定的最大值（图 1 (c)），从而避免了不同部分 softmax 计算间的频繁同步。而当小概率发生的输入超出给定范围时，「FlashDecoding++」对这一部分的 softmax 计算退化为原先的计算方法。

「矮胖」矩阵乘的优化

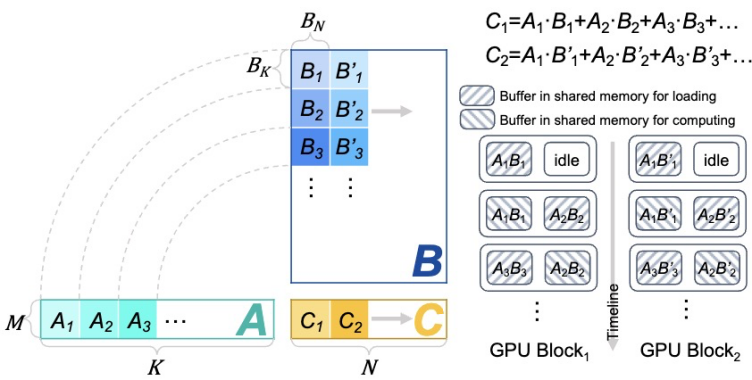
图 3 「矮胖」矩阵乘切分与双缓存机制

由于 Decode 阶段的输入为一个或几个 token 向量，因此该阶段的矩阵乘表现为「矮胖」形状。以矩阵 A×B=C 为例，A 与 B 矩阵的形状为 M×K 与 K×N，「矮胖」矩阵乘即 M 较小的情况。「FlashDecoding++」指出「矮胖」矩阵乘一般缓存受限，并提出双缓存机制等优化手段进行加速（图 3）。

图 4 自适应矩阵乘实现