LUCIDA：如何利用多因子策略构建强大的加密资产投资组合（因子合成篇）

书接上回，关于《用多因子模型构建强大的加密资产投资组合》系列文章中，我们已经发布了三篇：《理论基础篇》、《数据预处理篇》、《因子有效性检验篇》。

前三篇分别解释了多因子策略的理论与单因子测试的步骤。

一、因子相关性检验的原因：多重共线性

我们通过单因子测试部分筛选出一批有效因子，但以上因子不能直接入库。因子本身可以根据具体的经济含义进行大类划分，同类型的因子间存在较强的相关性，若不经相关性筛选直接入库，根据不同因子进行多元线性回归求预期收益率时，会出现多重共线性问题。计量经济学中，多重共线性是指回归模型中的一些或全部解释变量存在“完全”或准确的线性关系（各变量间高度相关）。

因此，有效因子筛选出后，首先需要根据大类对因子的相关性进行 T 检验，对于相关性较高的因子，要么舍弃显著性较低的因子，要么进行因子合成。

多重共线性的数学解释如下：

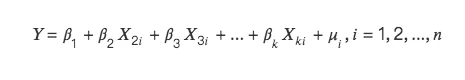
会存在两种情况：

多重共线性导致的后果：

1.完全共线性下参数估计量不存在

2.近似共线性下 OLS 估计量非有效

3.参数估计量经济含义不合理

4.变量的显著性检验（t 检验）失去意义

5.模型的预测功能失效：通过多元线性模型拟合出的预测收益率极其不准确，模型失效。

二、步骤一：同类型因子的相关性检验

检验新求出的因子与已入库因子的相关性。通常来说，有两类数据求相关性：

1.根据所有 token 在回测期间的因子值求相关

2.根据所有 token 在回测期间的因子超额收益值求相关

我们所求的每个因子对 token 的收益率都有一定的贡献和解释能力。进行相关性检验**，是为了找到对策略收益有不同解释和贡献的因子，策略的最终目的是收益**。如果两个因子对收益的刻画是相同的，即使两个因子值存在很大差别也无意义。因此，我们并不是想找到因子值本身差异大的因子，而是想找到因子对收益刻画不同的因子，所以最终选择了用因子超额收益值求相关。

我们的策略是日频，所以按回测区间的日期计算因子超额收益之间的相关系数矩阵

编程求解与库内相关最高的前 n 个因子：

def get_n_max_corr(self, factors, n= 1):
       factors_excess = self.get_excess_returns(factors)
       save_factor_excess = self.get_excess_return(self.factor_value, self.start_date, self.end_date)
       if len(factors_excess) < 1:
           return factor_excess, 1.0, None
       factors_excess[self.factor_name] = factor_excess[excess_return]
       factors_excess = pd.concat(factors_excess, axis= 1)
       factors_excess.columns = factors_excess.columns.levels[ 0 ]
       # get corr matrix
       factor_corr = factors_excess.corr()
       factor_corr_df = factor_corr.abs().loc[self.factor_name]
       max_corr_score = factor_corr_df.sort_values(ascending=False).iloc[ 1:].head(n)
       
       return save_factor_excess, factor_corr_df, max_corr_score

三、步骤二：因子取舍、因子合成

对于相关性较高的因子集合，可以采取两种方式处理：

（1）因子取舍

根据因子本身的 ICIR 值、收益率、换手率、Sharpe 比率，挑选某维度下最有效的因子进行保留，删除其他因子。

（2）因子合成

对因子集合中的因子进行合成，截面上尽可能多的保留有效信息

假设当前有 3 个待处理的因子矩阵：