FHE 是 ZK 的下一步 加密技术如是说

来源：佐爷歪脖山

加密货币的发展主线异常清晰，比特币创造了加密货币，以太坊创造了公链，泰达公司创造了稳定币，BitMEX 创造了永续合约，四种创造如同加密原语搭建出万亿的市场，数不清的暴富神话，或者被人时刻铭记的去中心化的迷梦。

加密技术的发展轨迹却不甚明了，各类共识算法，种种精巧的设计都敌不过质押和多签系统，而后者才是维持加密系统运转的真正支柱，比如抽去中心化质押的 WBTC 后，大部分 BTC L2 都无法存在，而 Babylon 的原生质押是这个方向的探索，价值 7 千万美元的探索。

我尝试在本文中勾勒一种加密技术的发展史，这区别于加密行业的各类技术变迁过程，比如 FHE 和 ZK 以及 MPC 的关系，从一个粗略应用的过程而言，MPC 用于开始，FHE 可以用于中间的计算过程，而 ZK 可以最终证明，而从应用时间顺序，则是 ZK 最早落地，之后 AA 钱包概念大火，MPC 作为一种技术方案得到重视，发展提速，唯独 FHE 在 2020 年已经被神施以喻言，但在 2024 年才略微起火。

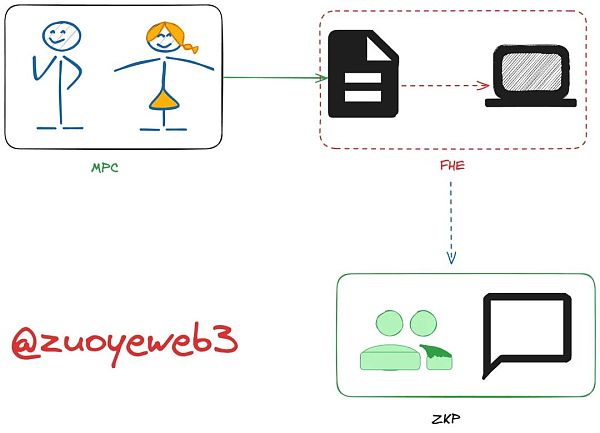
与 ZK 和 MPC 不同，FHE 甚至和当前所有的加密算法都不同，除了 FHE 之外，任何的对称或非对称加密技术，都在试图创造一个“不容易或无法破解的密码系统”来达到绝对的安全，但是 FHE 的目标是让加密后的密文发挥作用，即加密和解密是重要的，但是加密后，解密前的内容也不该浪费。

理论齐备，Web2 先于 Web3 落地

FHE 是一种基础技术，并且在学术上已经完成理论探索，Web2 巨头出力颇多，比如微软、英特尔、IBM 和 DARPA 支持的 Duality 已经进行软硬件适配和开发工具的准备。

有个好消息是，Web2 的巨头们也并不知道该拿 FHE 来做什么，Web3 从现在起步不算晚，还有一个坏消息是 Web3 的适配约等于 0，主流的比特币、以太坊都无法原生兼容 FHE 算法，尽管以太坊是世界计算机，但是硬算 FHE 恐怕要算到世界末日。

我们主要关注 Web3 的探索，只需要记住 Web2 巨头们对 FHE 非常热衷，并且已经做了大量基础工作即可。

这是因为 Vitalik 从 2020 年到 2024 年，重心都在 ZK 上。

这里要简单阐释下我对 ZK 的爆火归因，在以太坊确立以 Rollup 的扩容路线之后，ZK 的状态压缩功能可以极大减少 L2 向 L1 传输数据的大小，这在经济上具有巨大价值，当然，这只是理论上的，L2 的碎片化以及排序器等问题，甚至部分 L2/Rollup 收割用户手续费问题，这都属于发展中的新问题，只能用继续发展来解决。

简单归纳下，即以太坊需要扩容，确立了 Layer 2 发展路线，ZK/OP 系 Rollup 争奇斗艳，形成短期 OP，长期 ZK 的行业共识，塑造出 ARB/OP/zkSync/SatrkNet 四大巨头。

经济性是 ZK 能被加密世界，尤其是以太坊体系接纳的重要原因，甚至是唯一原因，因而接下来的 FHE 技术特点不会赘述，重点是考察 FHE 能在哪些方向提高 Web3 的运转效率，或者降低 Web3 的运作成本，降本和增效，总要占一个。

FHE 发展小史和成果

首先是区别同态加密和全同态加密，严格意义上而言，全同态加密是前者的一种特例，同态加密意味着“对密文的加法或乘法计算等同于对明文的加法或乘法计算”，即：

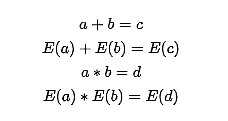
此时，c 和 E(c)，d 和 E(d) 可以视为等价值，但是要注意，这里的有两个难点：

明文和密文的相等，其实是明文在加入一些噪音后，对其进行进行运算得到密文，如果密文导致的偏离值过大，则会导致计算失败，因此控制噪音的各类算法的关键；

加法和乘法的开销巨大，密文计算可能是明文计算的 1 万到 100 万倍以上，而只有同时实现无限次的加法和乘法密文计算才能被称为全同态加密，当然，各类同态加密在各自领域也有其独特价值，按照实现程度的不同，可做如下划分：

部分同态加密（Partially homomorphic encryption）：只允许对加密数据执行有限的操作集，如加法或乘法。某种同态加密（Somewhat homomorphic encryption）：允许有限数量的加法和乘法运算。

全同态加密（Fully homomorphic encryption）：允许无限数量的加法和乘法运算，从而实现对加密数据的任意计算。

全同态加密（FHE）的发展历程可以追溯到 2009 年，Craig Gentry 首次提出了基于理想格的全同态算法，理想格是一种数学结构，它允许用户定义一个多维空间中的点集，其中这些点满足特定的线性关系。