IOSG Ventures：为什么FHE在Web3会有更好的应用前景？

原文作者：IOSG Ventures

隐私是人类和组织的基本权利。对个人而言，它帮助人们自由表达自己，而不必向第三方透露任何不想分享的信息。对于当今的大多数组织而言，数据被视为主要商品，数据隐私对于保护这一商品至关重要。密码朋克运动和数据商品化加速了密码学原语的研究和发展。

密码学是一个相当广泛的领域，当我们在计算的背景下看待密码学时，我们已经看到许多不同的方案，例如零知识证明、同态加密、Secret 共享等，这些方案自 1960 年代诞生以来一直在不断改进。这些方案对于解锁私人计算方法至关重要（数据之所以是是主要商品，那是因为人们可以从中发现生成洞察）。直到今天，Private 计算领域在多方计算和零知识证明方面有了显著发展，但输入数据本身始终存在隐私问题。

当最重要的商品公开时，任何数据所有者要在没有法律协议的情况下将此数据的计算外包出去是非常困难的。今天，每个人都依赖于数据隐私的合规标准，如针对健康数据的 HIPAA 和专门针对欧洲地区数据隐私的 GDPR 等。

在区块链领域，我们更相信技术的完整性，而不是监管机构的完整性。作为去许可和所有权最大化的信徒，如果我们相信用户拥有数据的未来，就需要无信任的方法来对这些数据进行计算。在 2009 年 Craig Gentry 的工作之前，在加密数据上执行计算这一概念一直没有突破。这是第一次有人能够在密文（即加密数据）上执行计算（加法和乘法）。

1. 全同态加密 (FHE) 的工作原理

那么，这种允许计算机在不了解输入的情况下执行计算的「魔法数学」到底是什么呢？

全同态加密（FHE）是一类加密方案，它允许在加密数据（密文）上执行计算而无需解密数据，为隐私和数据保护打开了一系列用例。

在 FHE 过程中，当数据被加密时，会向原始数据添加称为噪声的额外数据。这就是加密数据的过程。

每次执行同态计算（加法或乘法）时，都会添加额外的噪声。如果计算过于复杂，每次都添加噪声，最终解密密文就会变得非常困难（这在计算上非常繁重）。这种过程更适合加法，因为噪声呈线性增长，而对于乘法，噪声呈指数增长。因此，如果有复杂的多项式乘法，解密输出将非常困难。

如果噪声是主要问题，并且其增长使 FHE 变得难以使用，就必须加以控制。这催生了一种称为「Bootstrapping」的新过程。引导是一种使用新密钥对加密数据进行加密并在加密中解密的过程。这非常重要，因为它显著减少了计算开销以及最终输出的解密开销。虽然 Bootstrapping 减少了最终的解密开销，但在过程中会有大量的操作开销。这可能既昂贵又耗时。

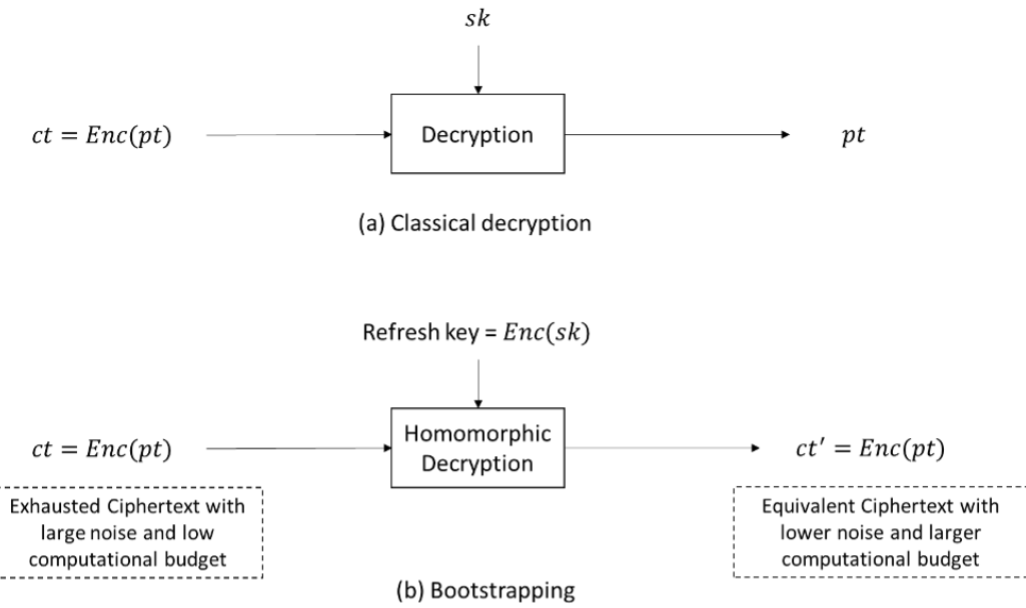
目前主要的 FHE 方案有：BFV、BGV、CKKS、FHEW、TFHE。除了 TFHE，这些方案的缩写都是其论文作者的名字。

可以将这些方案视为同一国家中讲的不同语言，每种语言都针对不同的优化。理想状态是统一这个国家，即所有这些语言都能被同一台机器理解。许多 FHE 工作组正在努力实现这些不同方案的可组合性。像 SEAL（结合 BFV 和 CKKS 方案）和 HElib（BGV + 近似数 CKKS）这样的库帮助实现 FHE 方案或不同计算的方案组合。例如，Zama 的 Concrete 库是一个针对 TFHE 的 Rust 编译器。

2. FHE 方案比较

下面是查尔斯·古特、迪米特里斯·穆里斯和奈克塔里奥斯·乔治·楚索斯在其论文《SoK：通过标准化基准对全同态加密库的新见解》SoK: New Insights into Fully Homomorphic Encryption Libraries via Standardized Benchmark（2022）中对不同库的性能比较。

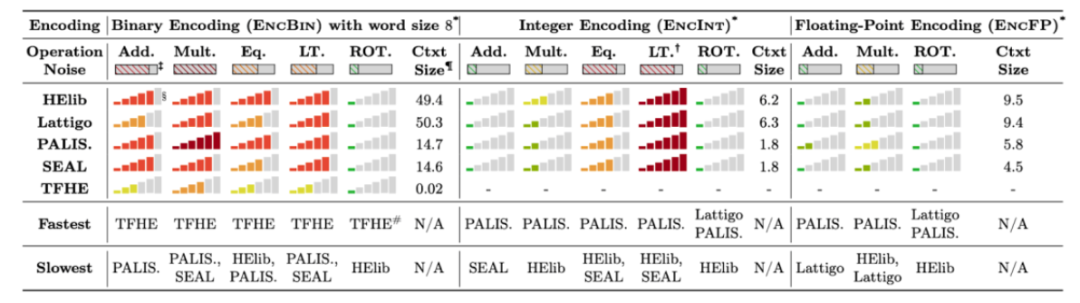
Web3 用例

当我们今天使用区块链和应用程序时，所有数据都是公开的，所有人都可以看到。这对大多数用例是有利的，但完全限制了许多需要默认隐私或数据保密的用例（例如机器学习模型、医疗数据库、基因组学、私人金融、不被操纵的游戏等）。FHE 支持的区块链或虚拟机本质上允许整个链的状态从起点开始加密，确保隐私，同时允许在加密数据上执行任意计算。所有存储或处理在 FHE 支持的区块链网络上的数据本质上是安全的。Zama 有一个 fhEVM 方案，允许在完全同态环境中进行 EVM 计算。这在执行层面为任何使用此库构建的 L1/L2 项目确保了隐私。尽管隐私链一直是很酷的技术，但采用率和代币表现并未显著提升。